The determination of the ground state of the carbon dioxide molecule is conducted through matrix Hartree-Fock computations for a polyatomic molecule. Utilization of basis sets is implemented to achieve a precision that approaches the sub-μ Hartree of the CO2 molecule for the energy levels. Utilizing a 28s14p14d14f atom-centered and a 24sl0plld bond-centered Gaussian basis set, the upper limit for the Hartree-Fock ground state energy of CO2 at its practical picture has been calculated, yielding a value of -187.125408 Hartree. Utilizing our knowledge in diatomic molecules, we approximate the precision of this measurement to fall within 5-6 μ Hartree. The current computations offer a methodology to assess the precision of different basis sets frequently utilized in molecular self-consistent field investigations. These basis sets encompass STOJG, 4-31G, 6-31G, 6-31G(3d), 6-31IG, 6-311+G(3d0, D95, and D95V+(3d)), alongside cc-pVDZ, uug-cc-pVDZ, cc-pVTZ, and aug-cc-pVTZ, which have been proposed for the purpose of investigating electron correlation. We have recently performed calculations on the CO1 ground state at the nuclear geomevy employed in the presenl work using the basis sets proposed by Dunning and co-workers and designated cc-pVQZ. aupcc-pVQZ, cc-pVSZ and nupcc-pVSZ. The estimated basis set truncation emrs for these sets are 0.00371, 0.003 19, 0.00047 and 0.00039 Hartree respectively.
| Published in | American Journal of Physical Chemistry (Volume 13, Issue 2) |
| DOI | 10.11648/j.ajpc.20241302.13 |
| Page(s) | 43-49 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Hartree-Fock Approximation, Polyatomic Molecules, CO2
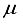 Hartree precision for monoatomic system operating under the Hartree-Fock framework. Progressing to the subsequent section, an examination was conducted on the employment of elliptical basis functions for diatomic molecules within the context of the Hartree-Fock model. Finally, the third section of the study demonstrated that through the integration of atom-centered and bond-centered functions within basis sets comprised of Gaussian-type functions, it is possible to achieve a level of accuracy that nears the sub-μ Hartree threshold for the total Hartree-Fock energy pertaining to the ground state of the nitrogen molecule.
Hartree precision for monoatomic system operating under the Hartree-Fock framework. Progressing to the subsequent section, an examination was conducted on the employment of elliptical basis functions for diatomic molecules within the context of the Hartree-Fock model. Finally, the third section of the study demonstrated that through the integration of atom-centered and bond-centered functions within basis sets comprised of Gaussian-type functions, it is possible to achieve a level of accuracy that nears the sub-μ Hartree threshold for the total Hartree-Fock energy pertaining to the ground state of the nitrogen molecule. 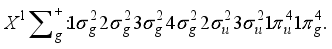 (1)
(1) 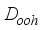 , which reflects its cylindrical symmetry along the molecular axis. Experimental measurements have determined the C=O bond lengths in CO2 to be approximately 1.160 Å
, which reflects its cylindrical symmetry along the molecular axis. Experimental measurements have determined the C=O bond lengths in CO2 to be approximately 1.160 Å 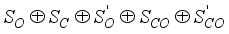 (2)
(2) 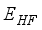 . Additionally, the parameters m and
. Additionally, the parameters m and 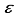 are utilized to signify the computational linear dependency present in the basis set. In particular, the symbol m is used to denote the count of eigenvalues pertaining to the overlap matrix that have magnitudes smaller than 10-5, while the symbol
are utilized to signify the computational linear dependency present in the basis set. In particular, the symbol m is used to denote the count of eigenvalues pertaining to the overlap matrix that have magnitudes smaller than 10-5, while the symbol 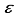 stands for the minimum eigenvalue. In prior research pertaining to the CO ground state, the basis set centered on the atom, identified as 30s15p15d15f, was utilized. The application of this basis set resulted in the determination of the Hartree-Fock energy for the ground state of CO, at the nuclear geometry in equilibrium according to experiments, exhibiting a deviation of 196
stands for the minimum eigenvalue. In prior research pertaining to the CO ground state, the basis set centered on the atom, identified as 30s15p15d15f, was utilized. The application of this basis set resulted in the determination of the Hartree-Fock energy for the ground state of CO, at the nuclear geometry in equilibrium according to experiments, exhibiting a deviation of 196 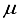 Hartree from the outcome derived from calculations based on finite differences
Hartree from the outcome derived from calculations based on finite differences 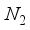 ground state compared to the finite difference outcome. The quantification of computational linear dependence was conducted as m = 5 and
ground state compared to the finite difference outcome. The quantification of computational linear dependence was conducted as m = 5 and 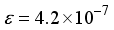 for CO, and m = 5 and
for CO, and m = 5 and 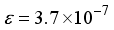 for
for 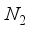 in these particular computations.
in these particular computations. 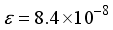 . Consequently, an examination was conducted on the antecedent basis set within the progression 2ns np nd nf, denoted as 28s14p14d14f. In the case of the CO (
. Consequently, an examination was conducted on the antecedent basis set within the progression 2ns np nd nf, denoted as 28s14p14d14f. In the case of the CO ( 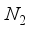 ), this particular basis set results in an energy discrepancy of 209 (227)
), this particular basis set results in an energy discrepancy of 209 (227) 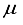 Hartree, where n = 4 (4) and
Hartree, where n = 4 (4) and 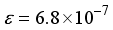 (
( 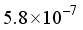 ). When using the 2Ss14p14d14f atom-centered basis set for CO2, the assessment of computational linear dependence was established through numerical values of m = 13 and
). When using the 2Ss14p14d14f atom-centered basis set for CO2, the assessment of computational linear dependence was established through numerical values of m = 13 and 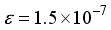 . A comparison of the energies calculated for CO1 with the 28s14p14d14f and the 30s15p15d15f atom-centered basis sets revealed a discrepancy of 23
. A comparison of the energies calculated for CO1 with the 28s14p14d14f and the 30s15p15d15f atom-centered basis sets revealed a discrepancy of 23 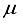 Hartree, whereas for CO (
Hartree, whereas for CO ( 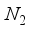 ), this difference was 13 (11)
), this difference was 13 (11) 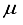 Hartree. A basis set acquired through the addition of a bond-centered set to the 28s14p14d14f atom-centered sets for CO was previously demonstrated to yield a Hartree-Fock energy deviating by merely 3.2
Hartree. A basis set acquired through the addition of a bond-centered set to the 28s14p14d14f atom-centered sets for CO was previously demonstrated to yield a Hartree-Fock energy deviating by merely 3.2 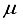 Hartree.
Hartree. Basie state | N | EHF (Hartree) | [m, ε] |
|---|---|---|---|
30s15p15d15f | 510 | -187.725114 | [15,8.4 (-8)] |
28s14p14d14f | 476 | -187.725091 | [13,1.5(-7)] |
28s14p:28s BC | 168 | -187.627251 | [5,4.5(-8)] |
28s 14p:26s BC | 166 | -187.627243 | [1,4.7(-6)] |
28s14p:26s BC | 208 | -187.718261 | [8,1.1(-7)] |
28s14p14d:25s 11p BC | 388 | -187.725259 | [5,2.1(-7)] |
28s14p14d:24s 11p 11d | 388 | -187.725259 | [5,2.1(-7)] |
28s14p14d 14f:24s 10p 11d BC | 585 | -187.725408 | [19,1.1(-7)] |
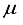 Hartree on a logarithmic scale. Upon analysis of these findings, it was deduced that a novel basis set should be formulated specifically for the CO2 molecule. Subsequently, the resolution was taken to establish the foundation for CO2 utilizing the 28s14p14d14f atom-centered groups.
Hartree on a logarithmic scale. Upon analysis of these findings, it was deduced that a novel basis set should be formulated specifically for the CO2 molecule. Subsequently, the resolution was taken to establish the foundation for CO2 utilizing the 28s14p14d14f atom-centered groups. 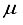 Hartree for CO compared to the finite difference outcome, and a difference of 49 821
Hartree for CO compared to the finite difference outcome, and a difference of 49 821 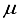 Hartree from the outcome achieved using the 28s14p14d14f atom-centered basis group. For the N2 molecule, the energy discrepancy resulting from the 30s15p:30s BC basis set in comparison to the finite difference outcome is 58008
Hartree from the outcome achieved using the 28s14p14d14f atom-centered basis group. For the N2 molecule, the energy discrepancy resulting from the 30s15p:30s BC basis set in comparison to the finite difference outcome is 58008 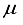 Hartree, and 57793
Hartree, and 57793 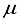 Hartree different from the 30s15p15d15f atom-centered basis set, In the case of CO2, utilizing the 28s14p: 28s BC basis set generates an energy value that surpasses the one derived from the 30s15p15d15f set by 97863
Hartree different from the 30s15p15d15f atom-centered basis set, In the case of CO2, utilizing the 28s14p: 28s BC basis set generates an energy value that surpasses the one derived from the 30s15p15d15f set by 97863 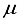 Hartree. This discrepancy in energy is illustrated by the second bar in Figure 1. However, a notable escalation in the realm of computational analysis, the presence of linear dependence becomes apparent in certain scenarios of the 28s14p: 28s BC basis set for CO, displaying values of [m,
Hartree. This discrepancy in energy is illustrated by the second bar in Figure 1. However, a notable escalation in the realm of computational analysis, the presence of linear dependence becomes apparent in certain scenarios of the 28s14p: 28s BC basis set for CO, displaying values of [m, 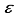 ] = [2, 3.5x10-6], in contrast to [5, 4.7 x10-8] for CO2. The elimination of the two most widely dispersed bond-center functions arise from the 28s14p: 28s BC basis set for CO2 resulted in a mere 8.4
] = [2, 3.5x10-6], in contrast to [5, 4.7 x10-8] for CO2. The elimination of the two most widely dispersed bond-center functions arise from the 28s14p: 28s BC basis set for CO2 resulted in a mere 8.4 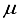 Hartree increase in energy, yet effectively decreased the metrics of the concept of computational linear dependence is crucial to understand to [m,
Hartree increase in energy, yet effectively decreased the metrics of the concept of computational linear dependence is crucial to understand to [m, 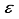 ] = [1, 5.0x10-6].
] = [1, 5.0x10-6]. 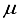 Hartree, while ensuring that the computational linear dependence remains within acceptable limits to preserve the numerical accuracy of the calculation. The incorporation of p-type functions into a 30s15p:30s BC basis set for N2 resulted in a set labeled as 30s15p:30s15p BC, leading to a reduction in energy of 53610
Hartree, while ensuring that the computational linear dependence remains within acceptable limits to preserve the numerical accuracy of the calculation. The incorporation of p-type functions into a 30s15p:30s BC basis set for N2 resulted in a set labeled as 30s15p:30s15p BC, leading to a reduction in energy of 53610 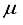 Hartree and a deviation of 440
Hartree and a deviation of 440 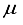 Hartree from the finite difference calculation. In the case of N2, 92.6% of the energy difference between using the 3Os15p:30s BC basis set and the finite difference energy can be accounted for by including p-symmetry bond-centered functions. This accounts for 93% of the discrepancy in energies calculated using the 30s15p:30s BC and the 30s15p15d15f basis sets. In the case of the CO2 ground state, the reduction in energy observed upon inclusion of a 14p BC set to the 28s14p:26s BC set corresponds to 92.8% of the difference between the energies computed with the 28s14p14d14f atom-centered set and the 28s14p:26s set. The third column depicted in Figure 1 illustrates the energy difference between the calculation with the 28s14p:26s14p BC basis set and our reference energy derived from the 30s15p15d15f basis set.
Hartree from the finite difference calculation. In the case of N2, 92.6% of the energy difference between using the 3Os15p:30s BC basis set and the finite difference energy can be accounted for by including p-symmetry bond-centered functions. This accounts for 93% of the discrepancy in energies calculated using the 30s15p:30s BC and the 30s15p15d15f basis sets. In the case of the CO2 ground state, the reduction in energy observed upon inclusion of a 14p BC set to the 28s14p:26s BC set corresponds to 92.8% of the difference between the energies computed with the 28s14p14d14f atom-centered set and the 28s14p:26s set. The third column depicted in Figure 1 illustrates the energy difference between the calculation with the 28s14p:26s14p BC basis set and our reference energy derived from the 30s15p15d15f basis set. 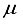 Hartree when compared to the 28s14p: 26s14p BC set. The energy derived from the 28s14p14d: 24sllp BC set is roughly ~146
Hartree when compared to the 28s14p: 26s14p BC set. The energy derived from the 28s14p14d: 24sllp BC set is roughly ~146 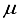 Hartree lower than the minimum energy documented in Table 1 for an atom-centered basis set (specifically, the 30s15p15d15f set). Moreover, the novel basis set constitutes only 68% of the magnitude of the atom-centered set, underscoring its heightened effectiveness. The fourth bar in Figure 1 illustrates the described outcome. Previous studies conducted on N2 revealed that the utilization of a 30s15p15d:30s15p BC basis set led to a Hartree-Fock energy that was lower compared to that achieved with a 0s15p15d15f basis set by approximately ~182
Hartree lower than the minimum energy documented in Table 1 for an atom-centered basis set (specifically, the 30s15p15d15f set). Moreover, the novel basis set constitutes only 68% of the magnitude of the atom-centered set, underscoring its heightened effectiveness. The fourth bar in Figure 1 illustrates the described outcome. Previous studies conducted on N2 revealed that the utilization of a 30s15p15d:30s15p BC basis set led to a Hartree-Fock energy that was lower compared to that achieved with a 0s15p15d15f basis set by approximately ~182 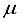 Hartree. Moreover, the energy acquired through the 30s15p15d:30s15p BC set was in close proximity to about ~ 42
Hartree. Moreover, the energy acquired through the 30s15p15d:30s15p BC set was in close proximity to about ~ 42 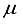 Hartree of the finite difference outcome. In contrast, in the case of CO, an energy calculation using a basis set denoted as 28s14p14d:28s14p BC resulted in an energy level that was roughly ~167
Hartree of the finite difference outcome. In contrast, in the case of CO, an energy calculation using a basis set denoted as 28s14p14d:28s14p BC resulted in an energy level that was roughly ~167 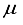 Hartree lower than the energy obtained with the 28s14p14d14f set. Nevertheless, it was approximately 455
Hartree lower than the energy obtained with the 28s14p14d14f set. Nevertheless, it was approximately 455 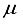 Hartree higher than the outcome obtained from employing the finite difference method.
Hartree higher than the outcome obtained from employing the finite difference method. 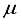 Hartree compared to the lowest energy value documented in Table 1 for a basis set centered on an atom. This outcome is depicted by the second-to-last bar in Figure 1. Regarding the fundamental state of the CO molecule, the basis set referred to as 30s15pl5dl5f:27s12pl0d10f BC produced energy approximately 195
Hartree compared to the lowest energy value documented in Table 1 for a basis set centered on an atom. This outcome is depicted by the second-to-last bar in Figure 1. Regarding the fundamental state of the CO molecule, the basis set referred to as 30s15pl5dl5f:27s12pl0d10f BC produced energy approximately 195 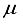 Hartree lower than that obtained with an atom-centered basis set (30s15p15d15f). Shifting focus to N2, the energy gap between the 30s15p15d15f and 30s15p15d15f:27s12pl0d BC sets is approximately 215
Hartree lower than that obtained with an atom-centered basis set (30s15p15d15f). Shifting focus to N2, the energy gap between the 30s15p15d15f and 30s15p15d15f:27s12pl0d BC sets is approximately 215 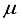 Hartree.
Hartree. Orbital | E (Hartree) |
|---|---|
-21.64836 | |
-21.64922 | |
-11.45880 | |
-1.63114 | |
-1.57732 | |
-0.90031 | |
-0.75389 | |
-0.72612 | |
-0.55513 |
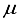 Hartree of the finite difference outcome. In the ultimate computation for the ground state of carbon dioxide, the basis set utilized was specified as 28s14p14d14f: 24s10pl1d BC. This computation yielded an energy that was 83
Hartree of the finite difference outcome. In the ultimate computation for the ground state of carbon dioxide, the basis set utilized was specified as 28s14p14d14f: 24s10pl1d BC. This computation yielded an energy that was 83 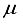 Hartree less than the energy acquired through the functions of symmetry belonging to s, p, and d orbitals are observed at both locations the atom and bond centers, and it was 394 Hartree lower than the reference energy acquired with the 30s15p15d15f atom-centered basis set. This outcome is depicted by the final bar in Figure 1. It is approximated that the computation utilizing the 28s14p14d14f: 24s10plld BC basis set, as detailed in Table 1 for the CO2 ground state, will entail an error of around 5-6
Hartree less than the energy acquired through the functions of symmetry belonging to s, p, and d orbitals are observed at both locations the atom and bond centers, and it was 394 Hartree lower than the reference energy acquired with the 30s15p15d15f atom-centered basis set. This outcome is depicted by the final bar in Figure 1. It is approximated that the computation utilizing the 28s14p14d14f: 24s10plld BC basis set, as detailed in Table 1 for the CO2 ground state, will entail an error of around 5-6 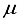 Hartree.
Hartree. 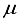 Hartree range. This accomplishment is deemed a notable progression in Hartree-Fock computations for multi-electron polyatomic molecules due to the unprecedented level of precision achieved. It is imperative to emphasize that the methodology adopted in this investigation is void of any presumptions that could impede the applicability of our approach to diverse polyatomic molecules.
Hartree range. This accomplishment is deemed a notable progression in Hartree-Fock computations for multi-electron polyatomic molecules due to the unprecedented level of precision achieved. It is imperative to emphasize that the methodology adopted in this investigation is void of any presumptions that could impede the applicability of our approach to diverse polyatomic molecules. sets | N (bash) | E (Hartree) | εBEST (Hartree) |
|---|---|---|---|
STO-3G | 15 | -185. 064 77 | 2.7608 |
3-12G | 27 | -186.661183 | 1.1645 |
4-21G | 27 | -187.427960 | 0.39785 |
6-31G | 27 | -187.614955 | 0.2114 |
6-31G(d) | 46 | -187.632837 | 0.0930 |
6-31G(2d) | 64 | -187.744122 | 0.0816 |
6-31G(3d) | 82 | -187.749958 | 0.0759 |
6-31G(3df) | 102 | -187.658690 | 0.0669 |
6-31G(3df) | 116 | -187.664131 | 0.0618 |
6-311G | 37 | -178.666217 | 0.1698 |
6-311+G(3df) | 118 | -187.808767 | 0.0619 |
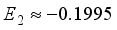 Hartree. This quantity represents only 7.5% of the pertinent error resulting from the truncation of the basis set, with the optimal truncation error
Hartree. This quantity represents only 7.5% of the pertinent error resulting from the truncation of the basis set, with the optimal truncation error 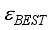 being 0.0813. The truncation error associated with the basis set 6-31G(2d) is measured at 0.0813 Hartree. The coefficients associated with the expansion of many-body perturbation theory are denoted as
being 0.0813. The truncation error associated with the basis set 6-31G(2d) is measured at 0.0813 Hartree. The coefficients associated with the expansion of many-body perturbation theory are denoted as 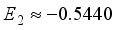 Hartree,
Hartree, 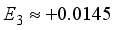 Hartree, and
Hartree, and 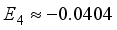 Hartree, respectively. Of particular interest is the observation that the magnitude of the coefficient E2 is -16% relative to E1, exceeding the values of the higher-order energy coefficients. Furthermore, the calculation of E3 is derived as -17.9% relative to E1, and E4 as -50% relative to E1. It is important to highlight that the specific numerical values assigned to E1, E2, E3, and E4 are not specified, having been excluded from the original inquiry. Nonetheless, this information affords a comprehensive understanding of the contrast between energy discrepancies and coefficients in the many-body perturbation approach for the STO-3G and 6-31G(2d) basis sets.
Hartree, respectively. Of particular interest is the observation that the magnitude of the coefficient E2 is -16% relative to E1, exceeding the values of the higher-order energy coefficients. Furthermore, the calculation of E3 is derived as -17.9% relative to E1, and E4 as -50% relative to E1. It is important to highlight that the specific numerical values assigned to E1, E2, E3, and E4 are not specified, having been excluded from the original inquiry. Nonetheless, this information affords a comprehensive understanding of the contrast between energy discrepancies and coefficients in the many-body perturbation approach for the STO-3G and 6-31G(2d) basis sets. | [1] | B. H. Wells and S. Wilson, J. Phys. 8: AI. Moi, Opt. Phys. 22 (1989) 1285. |
| [2] | J. W. Thompson and S. Wilson, J. Phys. B: At. Moi, Opt. Phys 23 (1990) 2205. |
| [3] | Moncrieff D and Wilson S 1993 J. Phys. 8: AI. Mol, Opl. Phys. 26 1605. |
| [4] | L. Laaksonen, B. P. Pyykk and D. Sundholm, Computer. Phys. Rep. 4 (1986) 313. |
| [5] | P. Pyylikb, Numerical Determination of the Electric Structure of Atom, Diatomic and Poly-atomic molecules (NATO AS1 Series (271) ed M Defranceschi and J. Delhalle p 161 (1989). |
| [6] | J. Kobus 1993 Chem. Phys. Len. 202(1993) 202. |
| [7] | D. Heinemann, A. Rosen and B. Fncke, Phys. Scr. 42 (1990) 692. |
| [8] | J. Kobus, D. Moncrieff and S. Wilson, J. Phys. B: At Mol. Opt. Phys. 27 (1994) 5139. |
| [9] | S. Hackel, D. Heinemann, D. Kolb and B. Fricke, Ctiem. Phys. Lett. 91(1993) 206. |
| [10] | I. M. Mills, 1974 Theoretical Chemistry (Specialist periodic Reports I ) 1 (1974) 110. |
| [11] | D. Moncrieff and S. Wilson, Chem. Phys. Lett. 209 (1993) 423. |
| [12] | D. Moncrieff and S. Wilson, Phys. B: Ar. Mol. Opt. Phys. 27 (1994) 1. |
| [13] | H. Preuss Z. Naturf 19a (1965) 1335. |
| [14] | S. Rothenberg and H. F. Schaefer, J. Chem. Phys. 54 (1971) 2765. |
| [15] | W. Butscher, S. Shih, R. J. Buenker and S. D. Peyerimhoff 1977 Chem. Phys. Lett. 52 (1977) 457. |
| [16] | D. Neisius and G. Verhaegen, Chem. Phys. Lett. 66 (2020) 358. |
| [17] | L. Lawlor, K. Vasudevan and F. Grein, Chem. Phys. Lett, 75 (2022) 79. |
| [18] | P. Crasky and M. Urban "Ab initio Calculations, Method and Application in Chemistry (Springer Lectures Notes in Chemistry 16) (Berlin: Springer) 2021. |
| [19] | P. Mach and O. Kysel, J. Comput. Chem. 6 (1985) 312. |
| [20] | E. R. Davidson and D. Feller, Chem. Rev. 86 (2023) 681. |
| [21] | J. M. L. Marlin, J. P. Francois and R. Gijbels, Comput. Chem. 10 (1985) 152. |
| [22] | J. M. L. Manin, J. P. Francois and R. Gijtels, J. Compul. Chem. 10 (1989)875. |
| [23] | J. M. L. Marlin, J. P. Francois and R. Gijbds, Theor. Chim. Acta 76 (1989) 195. |
| [24] | F. M. Tao and Y. K. Pan, J. Chem Phys. 97 (1992) 4989. |
| [25] | F. M. Tan and Y. K. Pan, Mol. Phys. 81 (1994) 507. |
| [26] | J. Kobus, D. Moncrieff and S. Wilson, J. Phys, B: At. Mol. Opt. Phys. 27 (2022) 2867. |
| [27] | M. J. Frisch et at., GAUSSIAN 92 Gaussian Inc. Pittsburgh (1992). |
| [28] | UNICHEM, Cray Research Inc version 2.3 (1994). |
| [29] | T. H. Jr. Dunning, J. Chem. Phys. 90 (2022) 1007. |
| [30] | D. E. Woon and T. H. Jr. Dunning, J. Chem. Phys. 100 (1994) 2975. |
| [31] | R. A. Kendall, T. H. Jr. Dunning and R. J. Harrison, J. Chem. Phys. 96 (2024) 6769. |
APA Style
Hasan, E. H., Abood, S. N. (2024). Utilizing the Hartree-Fock Method to Analyze Carbon Dioxide Molecule. American Journal of Physical Chemistry, 13(2), 43-49. https://doi.org/10.11648/j.ajpc.20241302.13
ACS Style
Hasan, E. H.; Abood, S. N. Utilizing the Hartree-Fock Method to Analyze Carbon Dioxide Molecule. Am. J. Phys. Chem. 2024, 13(2), 43-49. doi: 10.11648/j.ajpc.20241302.13
AMA Style
Hasan EH, Abood SN. Utilizing the Hartree-Fock Method to Analyze Carbon Dioxide Molecule. Am J Phys Chem. 2024;13(2):43-49. doi: 10.11648/j.ajpc.20241302.13
@article{10.11648/j.ajpc.20241302.13,
author = {Enass Hammadi Hasan and Saad Naji Abood},
title = {Utilizing the Hartree-Fock Method to Analyze Carbon Dioxide Molecule
},
journal = {American Journal of Physical Chemistry},
volume = {13},
number = {2},
pages = {43-49},
doi = {10.11648/j.ajpc.20241302.13},
url = {https://doi.org/10.11648/j.ajpc.20241302.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajpc.20241302.13},
abstract = {The determination of the ground state of the carbon dioxide molecule is conducted through matrix Hartree-Fock computations for a polyatomic molecule. Utilization of basis sets is implemented to achieve a precision that approaches the sub-μ Hartree of the CO2 molecule for the energy levels. Utilizing a 28s14p14d14f atom-centered and a 24sl0plld bond-centered Gaussian basis set, the upper limit for the Hartree-Fock ground state energy of CO2 at its practical picture has been calculated, yielding a value of -187.125408 Hartree. Utilizing our knowledge in diatomic molecules, we approximate the precision of this measurement to fall within 5-6 μ Hartree. The current computations offer a methodology to assess the precision of different basis sets frequently utilized in molecular self-consistent field investigations. These basis sets encompass STOJG, 4-31G, 6-31G, 6-31G(3d), 6-31IG, 6-311+G(3d0, D95, and D95V+(3d)), alongside cc-pVDZ, uug-cc-pVDZ, cc-pVTZ, and aug-cc-pVTZ, which have been proposed for the purpose of investigating electron correlation. We have recently performed calculations on the CO1 ground state at the nuclear geomevy employed in the presenl work using the basis sets proposed by Dunning and co-workers and designated cc-pVQZ. aupcc-pVQZ, cc-pVSZ and nupcc-pVSZ. The estimated basis set truncation emrs for these sets are 0.00371, 0.003 19, 0.00047 and 0.00039 Hartree respectively.
},
year = {2024}
}
TY - JOUR T1 - Utilizing the Hartree-Fock Method to Analyze Carbon Dioxide Molecule AU - Enass Hammadi Hasan AU - Saad Naji Abood Y1 - 2024/06/13 PY - 2024 N1 - https://doi.org/10.11648/j.ajpc.20241302.13 DO - 10.11648/j.ajpc.20241302.13 T2 - American Journal of Physical Chemistry JF - American Journal of Physical Chemistry JO - American Journal of Physical Chemistry SP - 43 EP - 49 PB - Science Publishing Group SN - 2327-2449 UR - https://doi.org/10.11648/j.ajpc.20241302.13 AB - The determination of the ground state of the carbon dioxide molecule is conducted through matrix Hartree-Fock computations for a polyatomic molecule. Utilization of basis sets is implemented to achieve a precision that approaches the sub-μ Hartree of the CO2 molecule for the energy levels. Utilizing a 28s14p14d14f atom-centered and a 24sl0plld bond-centered Gaussian basis set, the upper limit for the Hartree-Fock ground state energy of CO2 at its practical picture has been calculated, yielding a value of -187.125408 Hartree. Utilizing our knowledge in diatomic molecules, we approximate the precision of this measurement to fall within 5-6 μ Hartree. The current computations offer a methodology to assess the precision of different basis sets frequently utilized in molecular self-consistent field investigations. These basis sets encompass STOJG, 4-31G, 6-31G, 6-31G(3d), 6-31IG, 6-311+G(3d0, D95, and D95V+(3d)), alongside cc-pVDZ, uug-cc-pVDZ, cc-pVTZ, and aug-cc-pVTZ, which have been proposed for the purpose of investigating electron correlation. We have recently performed calculations on the CO1 ground state at the nuclear geomevy employed in the presenl work using the basis sets proposed by Dunning and co-workers and designated cc-pVQZ. aupcc-pVQZ, cc-pVSZ and nupcc-pVSZ. The estimated basis set truncation emrs for these sets are 0.00371, 0.003 19, 0.00047 and 0.00039 Hartree respectively. VL - 13 IS - 2 ER -